Plotter meets Python

Using the Python package pySerial, I was able to send commands to the plotter through just a couple of lines of code (see here):

# Open serial port
s = serial.Serial('/dev/wchusbserial1420', 115200)

# Wake up
s.write("\r\n\r\n")
time.sleep(2)       # wait for grbl to initialize 
s.flushInput()      # flush startup text in serial input

s.write("G21\n")   # units = mm
s.readline()

s.write("F5000\n") # speed = 5000 mm/min
s.readline()

s.write("S0 M5\n") # pen up
s.readline()

s.write("G01 X-10 Y-10\n") # go to (10, 10)
s.readline()

s.write("S1000 M3\n") # pen down
s.readline()

s.write("G01 X-20 Y-10\n") # go to (20, 10)
s.readline()

s.write("S0 M5\n") # pen up
s.readline()

This piece of code wakes up the plotter, raises the pen, moves to (10, 10) (note I wrote -10 for reasons described above), lowers the pen, moves to (20, 10) and finally raises the pen again. Effectively, this draws a straight line from (10mm, 10mm) to (20mm, 10mm).
Since I figured I would be needing this code more, I wrapped it in a function. I decided to go object-oriented and created classes Point and Line, respectively. For now, these classes only contained draw methods, but I knew more was going to be needed.

Lines and points

What seemed most intuitive to me was converting the SVG <path> element to G-code instructions. Such an element can contain various types of lines and curves that together create a connected (closed or open) path. A path like this can be constructed by tracing an image in a tool like Inkscape or Sketch. My final goal was to be able to plot Picasso’s drawing ‘Dog’, which could be traced with a single path.

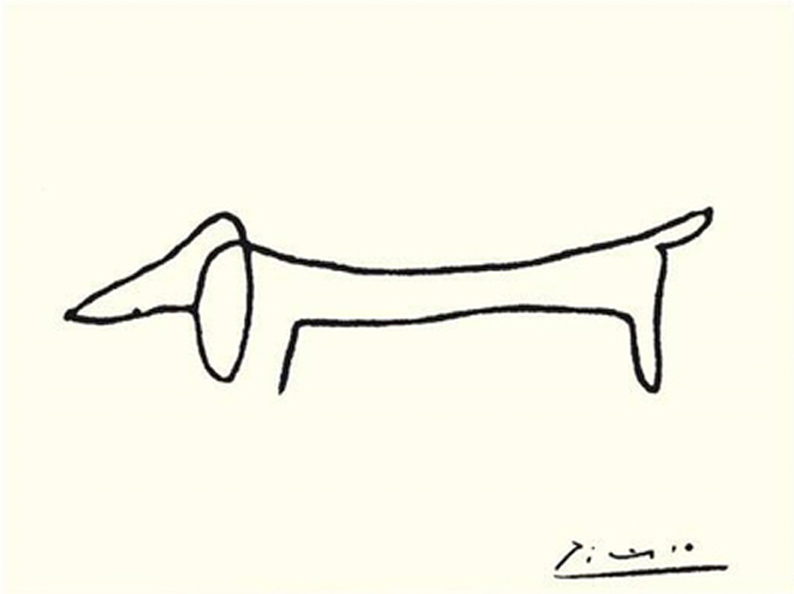
Dog (Picasso), pen on paper

An example of the SVG path syntax can be found on w3schools.
It turned out that parsing such a path was straightforward with regular expressions. There were three things that made things slightly more complicated.

1. Different instructions can have different numbers of parameters. For example, the M command (move) takes two numbers (an x and y coordinate), the Z (close path) command takes zero parameters, and some curve commands can take up to 7 parameters.
2. A command letter does not need to be repeated. For example, L 10 20 10 30 draws a line from the current position to (10, 20) and then another line to (10, 30) and is the same as L 10 20 L 10 30.
3. All commands can also be expressed with lower case letters, referring to relative instead of absolute positions. This requires a post processing step in which we keep track of the current position and add it if a relative position was supplied.

All of these issues were relatively easy to overcome, and after implementing this, I was able to parse an SVG file into a table which I could then convert to G-code. The code for this parser can be found on my GitHub.

Bézier curves

Still, I had only created code for drawing points and lines. To plot arcs, I could of course interpolate these using points, but the results were what I expected them to be: not very pretty. G-code supports circle arcs (an arc obtained by tracing part of a circle), so a better way would be to try to approximate the curves using circle arcs.
When tracing an image with a vector graphics tool like Sketch or Inkscape, the result will be a path consisting of Bézier curves. A Bézier curve is a parametric curve that can be described mathematically. I won’t go into more detail on Bézier curves; that is worth a blog post in itself. One thing that’s important to know is that there are quadratic and cubic Bézier curves. The quadratic curves are a special case of the cubic ones, so if I’m able to draw cubic Bézier curves I’m able to draw both.

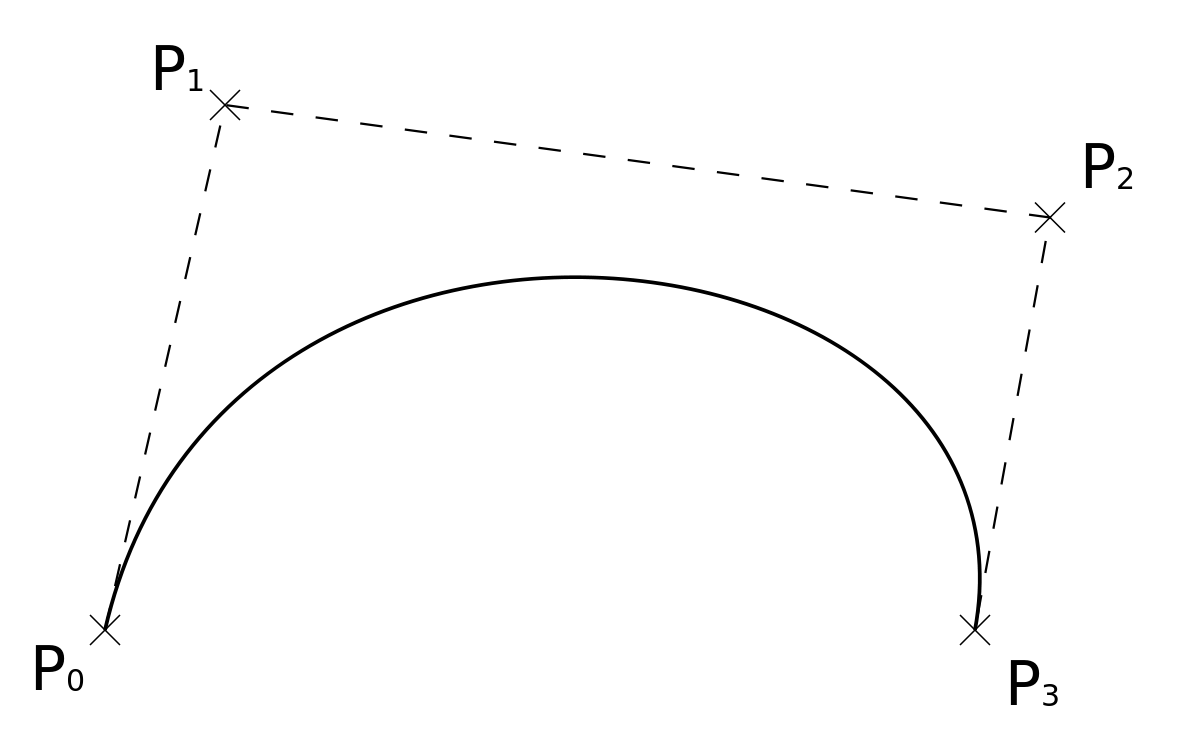
A cubic Bézier curve is defined by 4 points (source: Wikipedia)

It is in general not possible to convert a Bézier curve to a combination of circle arcs, but there are ways that are ‘good enough’. In particular, I implemented this approach in Python, which approximates a cubic Bézier curve with two circle arcs. I updated the classes for points and lines to include addition of points, multiplication of points with scalars, intersections of lines and so on. After these adjustments, it was relatively straightforward to write a CubicBezier class of which an instantiation could convert itself to two objects of class CircleArc.
For debugging purposes, I gave every such class a method that could draw the corresponding shape on a PyGame canvas. That way, I had a way of testing if everything worked without having to go through stacks of paper. In the end, this also allowed me to check if the thing I was going to plot looked the way it should, before actually sending it to the EleksDraw. For example, find below the code for Line.

import plotter as plt

class Line():
    # a line is defined by 2 points
    def __init__(self, point1, point2):
        self.P1 = point1
        self.P2 = point2
        
    def intersect(self, line2):
        # calculates the intersection point of the lines
        # solution is based on simple algebra
        a = self.P1.x - self.P2.x
        b = self.P1.y - self.P2.y

        u = (a*(line2.P2.y-self.P2.y) - b*(line2.P2.x-self.P2.x)) /\
            (a*(line2.P2.y-line2.P1.y) - b*(line2.P2.x-line2.P1.x))

        return (line2.P1.times(u)).plus(line2.P2.times(1-u))
    
    def perpendicular_at(self, P):
        U = Point(self.P2.y-self.P1.y, self.P1.x - self.P2.x)
        return Line(P, P.plus(U))
    
    def draw(self, canvas, color):
        pygame.draw.line(canvas, color,
                         (self.P1.x, canvas.get_height()-self.P1.y),
                         (self.P2.x, canvas.get_height()-self.P2.y))
        
    def plot_instructions(self):
        # assumes we are at P1
        return [plt.move(self.P2.x, self.P2.y)]

After all this work, I was finally able to plot Picasso’s dog.

Dog (Picasso/EleksDraw), pen on paper